research
The model suggests a clue as to when a pandemic will turn into an endemic
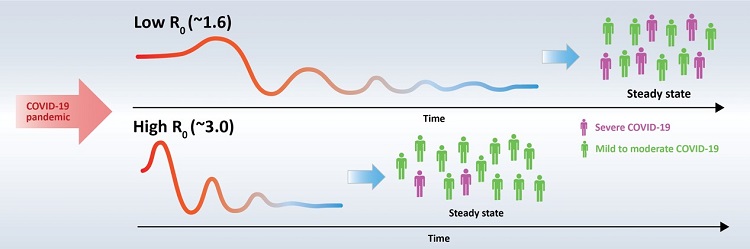
< In the study, courses of endemic transition of COVID-19 were estimated by mathematical modelling. The analysis shows an unexpected advantage of increased viral spread (high R0): a faster transition to the endemic phase with lower rates of severe COVID-19 and lower numbers of patients with severe COVID-19. Conditions in which viral spread (R0) increases include relaxing social distancing measures or the rise of variants with higher transmission rates like the Omicron variant. >
A mathematical model demonstrated that high transmission rates among highly vaccinated populations of COVID-19 ultimately reduce the numbers of severe cases. This model suggests a clue as to when this pandemic will turn into an endemic.
With the future of the pandemic remaining uncertain, a research team of mathematicians and medical scientists analyzed a mathematical model that may predict how the changing transmission rate of COVID-19 would affect the settlement process of the virus as a mild respiratory virus.
The team led by Professor Jae Kyoung Kim from the Department of Mathematical Science and Professor Eui-Cheol Shin from the Graduate School of Medical Science and Engineering used a new approach by dividing the human immune responses to SARS-CoV-2 into a shorter-term neutralizing antibody response and a longer-term T-cell immune response, and applying them each to a mathematical model. Additionally, the analysis was based on the fact that although breakthrough infection may occur frequently, the immune response of the patient will be boosted after recovery from each breakthrough infection.
The results showed that in an environment with a high vaccination rate, although COVID-19 cases may rise temporarily when the transmission rate increases, the ratio of critical cases would ultimately decline, thereby decreasing the total number of critical cases and in fact settling COVID-19 as a mild respiratory disease more quickly.
Conditions in which the number of cases may spike include relaxing social distancing measures or the rise of variants with higher transmission rates like the Omicron variant. This research did not take the less virulent characteristic of the Omicron variant into account but focused on the results of its high transmission rate, thereby predicting what may happen in the process of the endemic transition of COVID-19.
The research team pointed out the limitations of their mathematical model, such as the lack of consideration for age or patients with underlying diseases, and explained that the results of this study must be applied with care when compared against high-risk groups. Additionally, as medical systems may collapse when the number of cases rises sharply, this study must be interpreted with prudence and applied accordingly. The research team therefore emphasized that for policies that encourage a step-wise return to normality to succeed, the sustainable maintenance of public health systems is indispensable.
Professor Kim said, “We have drawn a counter-intuitive conclusion amid the unpredictable pandemic through an adequate mathematical model,” asserting the importance of applying mathematical models to medical research.
Professor Shin said, “Although the Omicron variant has become the dominant strain and the number of cases is rising rapidly in South Korea, it is important to use scientific approaches to predict the future and apply them to policies rather than fearing the current situation.”
The results of the research were published on medRxiv.org on February 11, under the title “Increasing viral transmission paradoxically reduces progression rates to severe COVID-19 during endemic transition.”
This research was funded by the Institute of Basic Science, the Korea Health Industry Development Institute, and the National Research Foundation of Korea.
-Publication
Hyukpyo Hong, Ji Yun Noh, Hyojung Lee, Sunhwa Choi, Boseung Choi, Jae Kyung Kim, Eui-Cheol Shin, “Increasing viral transmission paradoxically reduces progression rates to
severe COVID-19 during endemic transition,” medRxiv, February 9, 2022 (doi.org/10.1101/2022.02.09.22270633)
-Profile
Professor Jae Kyung Kim
Department of Mathematical Sciences
KAIST
Professor Eui-Cheol Shin
Graduate School of Medical Science and Engineering
KAIST
-
research KAIST leads AI-based analysis on drug-drug interactions involving Paxlovid
KAIST (President Kwang Hyung Lee) announced on the 16th that an advanced AI-based drug interaction prediction technology developed by the Distinguished Professor Sang Yup Lee's research team in the Department of Biochemical Engineering that analyzed the interaction between the PaxlovidTM ingredients that are used as COVID-19 treatment and other prescription drugs was published as a thesis. This paper was published in the online edition of 「Proceedings of the National Academy of Sciences of Ameri
2023-03-16 -
research Research Finds Digital Music Streaming Consumption Dropped as a Result of Covid-19 and Lockdowns
Decline in human mobility has stunning consequences for content streaming The Covid-19 pandemic and lockdowns significantly reduced the consumption of audio music streaming in many countries as people turned to video platforms. On average, audio music consumption decreased by 12.5% after the World Health Organization’s (WHO) pandemic declaration in March 2020. Music streaming services were an unlikely area hit hard by the Covid-19 pandemic. New research in Marketing Science found that
2022-02-15 -
fund Seegene Opens Covid-19 Testing Mobile Station on Campus
Seegene donates testing reagents for 40,000 people with results available in three hours Seegene, a molecular diagnostic testing company, donated enough testing reagents for 40,000 COVID-19 tests for the KAIST community and set up a mobile testing station run by the Seegene Medical Foundation on October 28. The entire COVID-19 diagnosis process, including specimen collection, PCR testing, and results analysis, can be conducted at the mobile testing unit developed by Seegene. The on-site tes
2021-11-03 -
event MCM Utilized at Residential Treatment Center in Gyeonggi
The Mobile Clinic Module (MCM) developed by the KAIST Action for Respiratory Epidemics was installed at special residential treatment center in Gyeonggi Province on September 13. The MCM is an isolate negative pressure unit fitted with high-quality medical equipment, developed by Professor Taek-Jin Nam of the Department of Industrial Design under the KAIST New Deal R&D Initiative. This is also a part of the Korean Disease Control Package Development Project from last July. In January, a
2021-09-15 -
research A Study Reveals What Triggers Lung Damage during COVID-19
A longitudinal study of macrophages from SARS-CoV-2 infected lungs offers new insights into dynamic immunological changes A KAIST immunology research team found that a specific subtype of macrophages that originated from blood monocytes plays a key role in the hyper-inflammatory response in SARS-CoV-2 infected lungs, by performing single-cell RNA sequencing of bronchoalveolar lavage fluid cells. This study provides new insights for understanding dynamic changes in immune responses to COVID-1
2021-08-04