research
Mathematical Principle behind AI's 'Black Box'
View : 5837
Date : 2018-09-12
Writer : ed_news

(from left: Professor Jong Chul Ye, PhD candidates Yoseob Han and Eunju Cha)
A KAIST research team identified the geometrical structure of artificial intelligence (AI) and discovered the mathematical principles of highly performing artificial neural networks, which can be applicable in fields such as medical imaging.
Deep neural networks are an exemplary method of implementing deep learning, which is at the core of the AI technology, and have shown explosive growth in recent years. This technique has been used in various fields, such as image and speech recognition as well as image processing.
Despite its excellent performance and usefulness, the exact working principles of deep neural networks has not been well understood, and they often suffer from unexpected results or errors. Hence, there is an increasing social and technical demand for interpretable deep neural network models.
To address these issues, Professor Jong Chul Ye from the Department of Bio & Brain Engineering and his team attempted to find the geometric structure in a higher dimensional space where the structure of the deep neural network can be easily understood. They proposed a general deep learning framework, called deep convolutional framelets, to understand the mathematical principle of a deep neural network in terms of the mathematical tools in Harmonic analysis.
As a result, it was found that deep neural networks’ structure appears during the process of decomposition of high dimensionally lifted signal via Hankel matrix, which is a high-dimensional structure formerly studied intensively in the field of signal processing.
In the process of decomposing the lifted signal, two bases categorized as local and non-local basis emerge. The researchers found that non-local and local basis functions play a role in pooling and filtering operation in convolutional neural network, respectively.
Previously, when implementing AI, deep neural networks were usually constructed through empirical trial and errors. The significance of the research lies in the fact that it provides a mathematical understanding on the neural network structure in high dimensional space, which guides users to design an optimized neural network.
They demonstrated improved performance of the deep convolutional framelets’ neural networks in the applications of image denoising, image pixel in painting, and medical image restoration.
Professor Ye said, “Unlike conventional neural networks designed through trial-and-error, our theory shows that neural network structure can be optimized to each desired application and are easily predictable in their effects by exploiting the high dimensional geometry. This technology can be applied to a variety of fields requiring interpretation of the architecture, such as medical imaging.”
This research, led by PhD candidates Yoseob Han and Eunju Cha, was published in the April 26th issue of the SIAM Journal on Imaging Sciences.
Figure 1. The design of deep neural network using mathematical principles
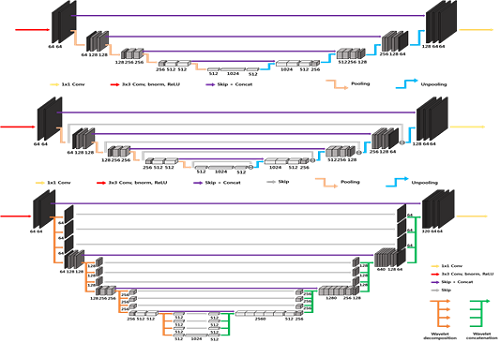
Figure 2. The results of image noise cancelling

Figure 3. The artificial neural network restoration results in the case where 80% of the pixels are lost

Releated news
- No Data